An airplane weighing 5000 lb is flying at standard sea level with a velocity of 200 mi/h. At this velocity, the L/D ratio is a maximum. The wing area and aspect ratio are 200 ft.2 and 8.5, respectively. The Oswald efficiency factor is 0.93. Calculate the total drag on the airplane.

- Consider an airplane patterned after the Fairchild Republic A-10, a twin-jet attack aircraft. The airplane has the following characteristics: wing area = 47 m2, aspect ratio = 6.5, Oswald efficiency factor = 0.87, weight = 103,047 N, and parasite drag coefficient =0.032. The airplane is equipped with two jet engines with 40,298 N of static thrusts each at sea level.
- Calculate and sketch the power required curve at sea level.
- Calculate the maximum velocity at sea level.
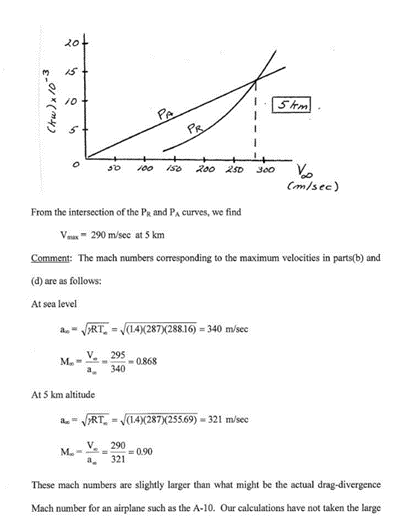
- Calculate and plot the power required curve at 5 km altitude.
- Calculate the maximum velocity at 5 km altitude. (Assume the engine thrust varies directly with free stream density.)




- V-tailed, single engine light private airplane. The characteristics of the airplane are as follows: aspect ratio = 6.2, wing area = 181 ft.2, Oswald efficiency factor = 0.91, weight = 3000 lb, and parasite drag coefficient = 0.027. The airplane is powered by a single piston engine of 345 hp maximum at sea level. Assume the power of the engine is proportional to free stream density. The two-bladed propeller has an efficiency of 0.83.
- Calculate the power required at sea level.
- Calculate the maximum velocity at sea level.
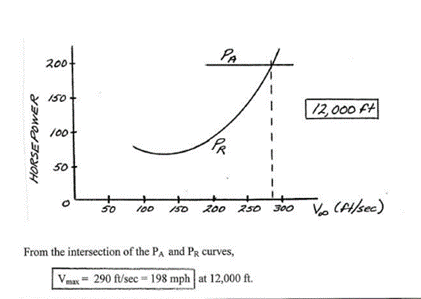
- Calculate the power required at 12,000 ft. altitude.
- Calculate the maximum velocity at 12,000 ft. altitude.