Application of 1st Order Differential Equation
Laws of growth and decay/decomposition of growth/Radioactive decay

Population 60 000 in 1990, increased to 63 000 by 2000. Estimate the population in 2010.

Logistic Growth Equation and Analytic Solution

Use the exact solution to determine when the population will reach 450. Po = 500. Logistic growth?


Logistic Equation and Models For Population
Differential equation solve. Logistic Equation and Models For Population.
Biologist stock a lane with 500 fish and estiamte the carrying capacity to be 10,000. The number of fish tripled during the first year.
Assuming that the size of the fish population satisfies the logistic equation, find an expression for the size of the population after w years.


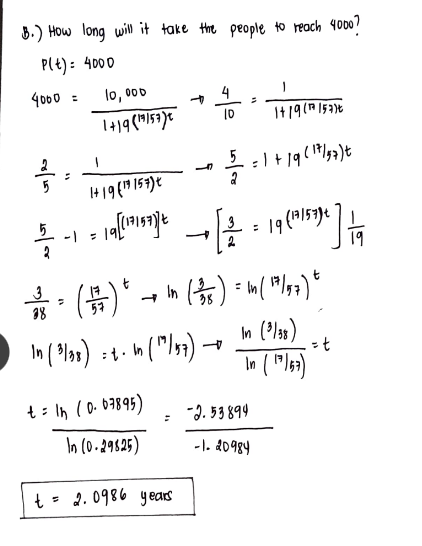
Population Growth: Exponential

Population Growth: Exponential/
A population that starts with 500 people, increases by 15% in 10 years. What is the population in 30 years?
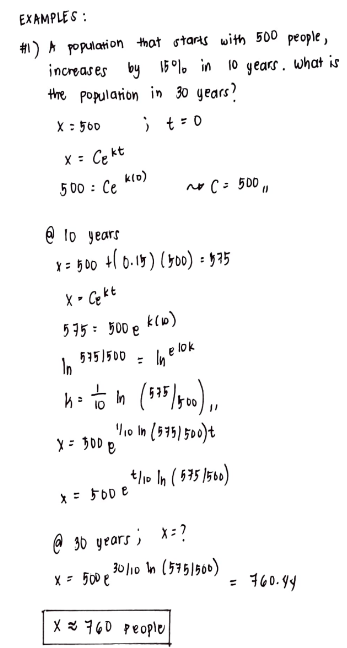

It is known that the population of a certain country at time t is proportional to the people living in it presently. If after 2 years, the population is tripled the original, find the number of people initially.

https://googleads.g.doubleclick.net/pagead/ads?client=ca-pub-4992295247869184&output=html&h=280&slotname=3523241294&adk=1745771614&adf=3408513213&pi=t.ma~as.3523241294&w=1140&fwrn=4&fwrnh=100&lmt=1678887284&rafmt=1&format=1140×280&url=https%3A%2F%2Ftheskyscorner.com%2Fapplication-of-1st-order-differential-equation-2%2F&host=ca-host-pub-2644536267352236&fwr=0&fwrattr=true&rpe=1&resp_fmts=3&wgl=1&adsid=ChEI8NnFoAYQmbznopqLlqmFARI5APsQfT7qNVKC6dPJZaBpXGIs9aMmM0L5UHzMmBuONKoP5JKQ0vG8mjLAa7NMiieL-_5qxooprtE2&uach=WyJXaW5kb3dzIiwiMTAuMC4wIiwieDg2IiwiIiwiMTExLjAuNTU2My42NSIsW10sZmFsc2UsbnVsbCwiNjQiLFtbIkdvb2dsZSBDaHJvbWUiLCIxMTEuMC41NTYzLjY1Il0sWyJOb3QoQTpCcmFuZCIsIjguMC4wLjAiXSxbIkNocm9taXVtIiwiMTExLjAuNTU2My42NSJdXSxmYWxzZV0.&dt=1678887279058&bpp=4&bdt=826&idt=168&shv=r20230313&mjsv=m202303070101&ptt=9&saldr=aa&abxe=1&cookie=ID%3D6cd1f1ff6279f1cc-2242116981d1006a%3AT%3D1648817502%3ART%3D1648817502%3AS%3DALNI_Ma9X2EQPzgi9Yop6bNYKYchVVZSQg&gpic=UID%3D000007e1014b904d%3AT%3D1658289413%3ART%3D1678882871%3AS%3DALNI_MbfQlk3wHmEW6CqU9kfpAzoAYs2aw&prev_fmts=1140×280&correlator=3861810458241&frm=20&pv=1&ga_vid=168115324.1648817501&ga_sid=1678887279&ga_hid=1786186301&ga_fc=1&u_tz=480&u_his=1&u_h=864&u_w=1536&u_ah=824&u_aw=1536&u_cd=24&u_sd=1&dmc=8&adx=380&ady=7449&biw=1899&bih=902&scr_x=0&scr_y=3848&eid=44759837%2C44777877%2C44759876%2C44759927%2C31072915%2C31072951%2C44774606%2C44786424%2C31071976%2C31072922&oid=2&pvsid=2836572455616639&tmod=1041978388&uas=3&nvt=1&ref=https%3A%2F%2Ftheskyscorner.com%2Fwp-admin%2Fedit.php%3Fpost_status%3Dpublish%26post_type%3Dpage%26orderby%3Ddate%26order%3Ddesc&fc=1920&brdim=0%2C0%2C0%2C0%2C1536%2C0%2C1536%2C824%2C1920%2C902&vis=1&rsz=%7C%7CoeEbr%7C&abl=CS&pfx=0&fu=128&bc=31&jar=2023-03-10-01&ifi=3&uci=a!3&btvi=2&fsb=1&xpc=34qYhU3vQ8&p=https%3A//theskyscorner.com&dtd=5099
Laws of Growth and Decay

Differential equation. Laws of growth and decay.
Radium decomposes at the air at the rate proportional to the present amount. If initially there are 20 grams, and after 10 years, 06% of the original amount decomposed.
A. Set a model that will predict the amount of radium at any time t.

What is the half life of the radium?
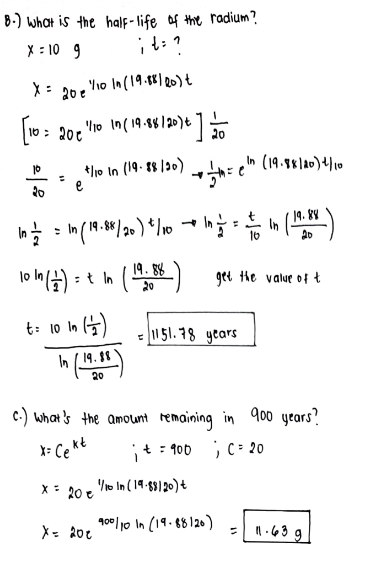



Radium decomposes at a rate proportional to the amount present. If the half life is 1600 years, find the percentage remaining at the end of 200 years.


Continuous Compound Interest

Compound interest and differential equation.
If the nominal interest rate is 3%, how much is 5000 pesos worth in 10 years in a continuously compounded account?


How long will it take a bank deposit to double if interest is compounded continuously at a constant rate of 4% per annum?
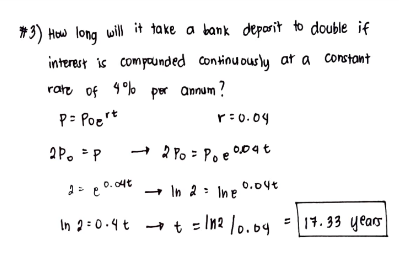
A depositor places 10 000 dollars in a certificate of deposit account which pays 7% interest per annum compounded continuously. How much will be in the account after two years.

Newton’s Law of Cooling



A thermometer reading 10 Celsius is brought in a room whose temperature is 18 C. One minute later, the thermometer reading is 14 C. How long does it takes until the reading becomes 16 C?


A metal is heated up to a temperature of 500 Celsius. It is then exposed to a temperature of 38 C. After 2 minutes, the temperature is 190 C. What is the time required to be in 100 C?




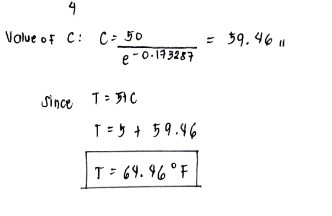



A tank contains 1 500 L of water and 20 kg of dissolved salt. Fresh water is entering the tank at 15 L/min, and the solution drains at a rate of 10 L/min. How much salt is in the tank at t minutes and at 10 minutes.


Electrical Circuit




