Skip to content

Sizing Matrix And Carpet Plots For Aircraft Optimization

Introduction about the Empty Weight Estimation and Refined Sizing

The empty weight of the airplane was calculated using the statistical group weights method by a detailed estimation of the weight of each component of the aircraft. With an initial estimate of π‘Šπ‘œ (as drawn) and π‘Šπ‘’ (as drawn), we can calculate the fuel weight π‘Šπ‘“ by using the refined sizing analysis. The following formulas can be used:

To get the new value of Wo:

π‘Šπ‘œ = π‘Šπ‘’,π‘Žπ‘  π‘‘π‘Ÿπ‘Žπ‘€π‘› + π‘Šπ‘“ + π‘Šπ‘ + π‘Šp

To get the new value of We:

To get the new value of We. Empty weight estimation of aircraft
  1. Sizing Matrix for Aircraft Optimization

The sizing procedure described ensures that the as-drawn aircraft will meet the required mission range or other important performance criteria. The configuration geometry was initially selected to meet the requirements based on assumptions for lift, drag, thrust, etc.

Sizing Matrix And Carpet Plots For Aircraft Optimization
  1. Sizing Matrix Method
  2. Purpose
    1. To identify what combination of 𝑇 π‘Š (or 𝑃 π‘Š) and π‘Š 𝑆 will meet all the requirements at minimum weight.

Sizing Matrix

  • Thrust-to-weight ratio 𝑇/π‘Š (or power-to-weight ratio; 𝑃/π‘Š) and wing loading π‘Š/𝑆 are varied from the baseline values (typically Β± 20 %).
  • Each combination of 𝑇/π‘Š (or 𝑃/π‘Š) and π‘Š/𝑆 produces a different airplane with different aerodynamics, propulsion, and weights. Size each of the airplanes separately to determine the takeoff weight of each to perform the design mission.
  • Analyze each combination separately for performance. If the 𝑇/π‘Š (or 𝑃/π‘Š) and π‘Š/𝑆 variations are wide enough, at least one aircraft will meet the requirements.
Sizing Matrix And Carpet Plots For Aircraft Optimization weight estimation

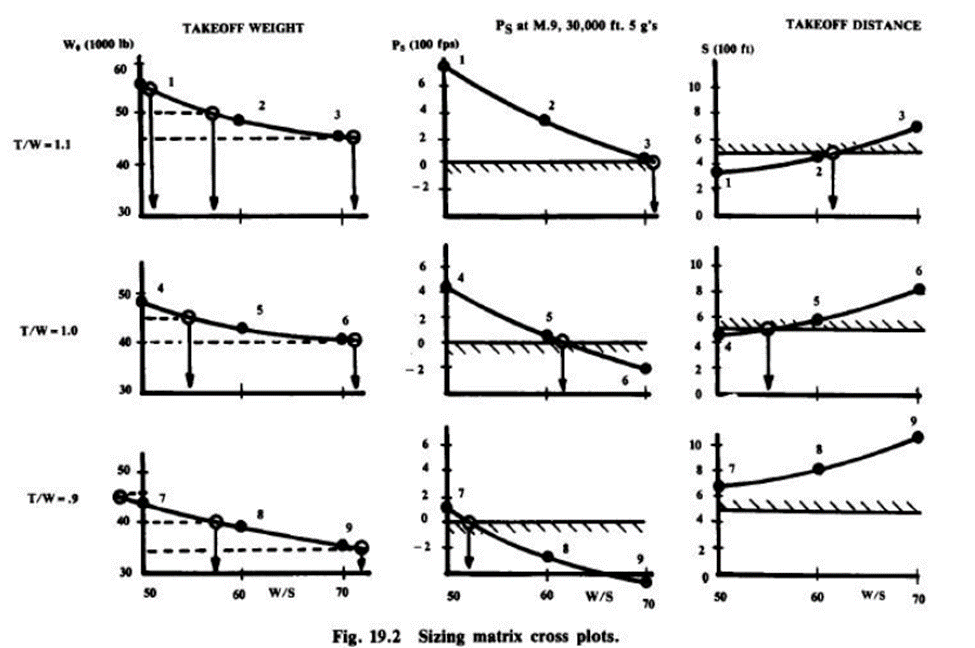
Sizing Matrix Cross Plot

  • Start optimization of 𝑇/π‘Š (or 𝑃/π‘Š) and π‘Š/𝑆 by cross-plotting the sizing matrix data in terms of chosen performance characteristics and takeoff weights.
  • From the takeoff weight graphs, wing loadings corresponding to regularly spaced arbitrary gross weights are determined.
  • 𝑇/π‘Š (or 𝑃/π‘Š) and π‘Š/𝑆 values for the arbitrary gross weights are transferred to a π‘Š/𝑆 – 𝑇/π‘Š (or 𝑃/π‘Š) graph.
  • Smooth curves are drawn connecting various points with identical gross weight to produce lines of constant takeoff gross weight.
  • From these curves, it is possible to determine the sized takeoff weight for any combination of π‘Š/𝑆 and 𝑇/π‘Š (or 𝑃/π‘Š).
  • π‘Š/𝑆 values that exactly meet various performance requirements are obtained from the performance plots for different 𝑇/π‘Š (or 𝑃/π‘Š) values.
  • The combinations of 𝑇/π‘Š (or 𝑃/π‘Š) and π‘Š/𝑆 that exactly meet a performance requirement are transferred to the π‘Š/𝑆 – 𝑇/π‘Š (or 𝑃/π‘Š) graph and connected by smooth curves.
  • The desired solution is the lightest aircraft that meets all the requirements. It is usually a combination where two constraint lines meet.
Sizing Matrix And Carpet Plots For Aircraft Optimization weight estimation

Using the data from the sizing matrix plot, we can conclude the following approximations:

  • πΆπ·π‘œ~𝑆𝑀𝑒𝑑 due to wing area and nacelle size variations.
  • 𝑆𝑀𝑒𝑑,𝑀𝑖𝑛𝑔~𝑆.
  • 𝑀𝑒𝑑,π‘›π‘Žπ‘π‘’π‘™π‘™π‘’~𝑇.
  • 𝐢𝐷,π‘€π‘Žπ‘£π‘’ must be recalculated.
  • 𝑆𝑀𝑖𝑛𝑔,π‘π‘Ÿπ‘œπ‘ π‘  π‘ π‘’π‘π‘‘π‘–π‘œπ‘›~𝑆𝑀𝑖𝑛𝑔.
  • Variation in 𝐾 may be neglected but if the wing area changes, the airplane will fly at a different 𝐢𝐿 , effecting 𝐾.
  • π‘Šπ‘€π‘–π‘›π‘”~𝑆𝑀𝑖𝑛𝑔 0.7 (same holds for tail surfaces).
  • π‘Šπ‘’π‘›π‘”π‘–π‘›π‘’~𝑇 1.1 .
  • Β π‘‡π‘–π‘›π‘ π‘‘π‘Žπ‘™π‘™π‘’π‘‘~π‘‡π‘’π‘›π‘–π‘›π‘ π‘‘π‘Žπ‘™π‘™ed.
Sizing Matrix And Carpet Plots For Aircraft Optimization weight estimation

Carpet Plots

Another presentation format for the sizing matrix, the so-called “carpet plot,” is based upon superimposing the takeoff weight plots.

Sizing Matrix And Carpet Plots For Aircraft Optimization weight estimation

Steps:

  • Plot π‘Šπ‘œ as a function of π‘Š 𝑆 for say 𝑇 π‘Š = 1.1,
  • Plot π‘Šπ‘œ as a function of π‘Š 𝑆 for say 𝑇 π‘Š = 1.0.
  • To avoid clutter, you may shift the horizontal axis to left by some arbitrary distance.
  • Plot π‘Šπ‘œ as a function of π‘Š 𝑆 for say 𝑇 π‘Š = 0.9, again shifting the horizontal axis.
  • Mark and connect with smooth constraint lines, the wing loadings that exactly meet requirements, say takeoff distance, 𝑃𝑠 and acceleration time.
Sizing Matrix And Carpet Plots For Aircraft Optimization weight estimation

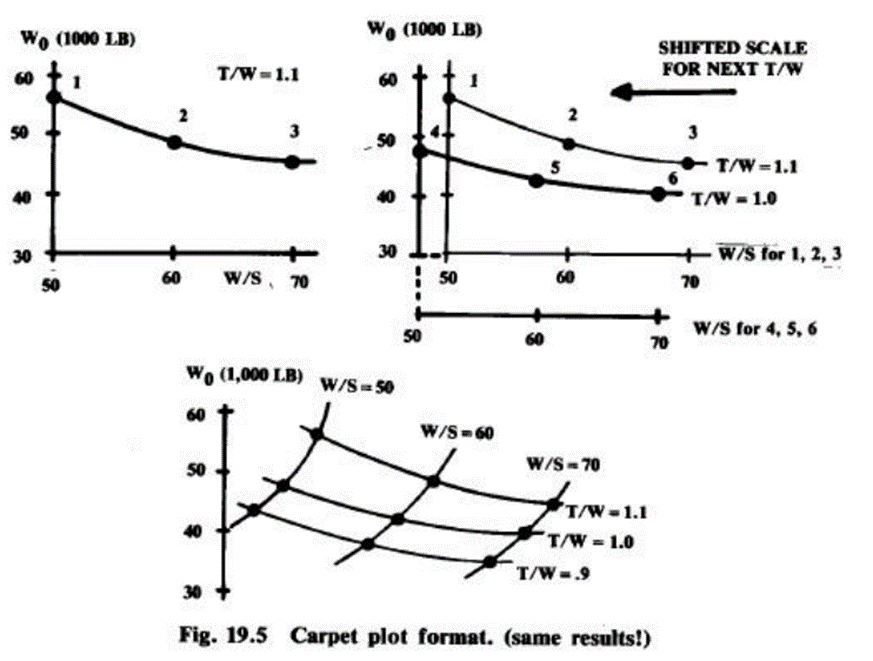
The optimal airplane is the one corresponding to the lowest point on the curve that meets all the constraints. It is possible to create carpet plots in which the figure of merit is the cost rather than the weight. For most airplane types minimization of weight will also minimize the cost.

Sizing Matrix And Carpet Plots For Aircraft Optimization weight estimation

References

Γ–zgen, P. D. (n.d.). Metu.edu. Retrieved from The philosophy of airplane design: http://ae.metu.edu.tr/~ae452sc2/lecture7_sizing_matrix_carpet_plots.pdf

Raymer, D. P. (n.d.). Aircraft Design: A Conceptual Approach .

sections, T. o., & data, i. a. (n.d.). Ira Abbott. McGraw-Hill, New York, 1949.

Spieck, M. (n.d.). 5 Main Characteristics of an Aircraft Design Process. Retrieved from Research Gate: https://www.researchgate.net/figure/Main-Characteristics-of-an-Aircraft-Design-Process_fig3_36421809

Thickness-chord ratio. (n.d.). Retrieved from Dictionary: https://encyclopedia2.thefreedictionary.com/thickness%2Fchord+ratio

Leave a Reply

Your email address will not be published.